Παραδείγματα θεμάτων

Ποδοσφαιρική Φανέλα

(Βαθμός δυσκολίας: Eύκολο)

O Λουκάς ετοιμάζει την τσάντα ποδοσφαίρου του .Πρέπει να διαλέξει μια φανέλα για να φορέσει στον αγώνα. 

Φανέλα Α	Φανέλα Β	Φανέλα Γ	Φανέλα Δ

Η φανέλα που θα διαλέξει πρέπει να έχει χρωματιστά μανίκια, μαύρο κολάρο και καθόλου ρίγες.

Ερώτηση:
Ποιά φανέλα θα διαλέξει ο Λουκάς;

Απάντηση:
A. Την φανέλα Α     
B. Την φανέλα Β    
Γ. Την φανέλα Γ
Δ. Την φανέλα Δ

Λύση:
Η απάντηση Β είναι σωστή.

Εξήγηση:
Η φανέλα Α δεν είναι σωστή επειδή η έχει μαύρα μανίκια και λευκό κολάρο.
Η φανέλα Β είναι σωστή επειδή έχει χρωματιστά μανίκια, μαύρο κολάρο και δεν έχει ρίγες.
Η φανέλα Γ δεν είναι σωστή επειδή έχει ρίγες.
Η φανέλα Δ δεν είναι σωστή επειδή έχει μαύρα μανίκια και λευκό κολάρο.

Σήματα Καπνού

(Βαθμός δυσκολίας: Mέτριο)

Η Μετεωρολόγος Κάστορας χρησιμοποιεί σήματα καπνού για να στείλει μηνύματα από την κορυφή του βουνού στους κάστορες που βρίσκονται στην πεδιάδα.

Χρησιμοποιεί μικρά και μεγάλα σύννεφα καπνού και τον παρακάτω κώδικα για να στείλει τα μηνύματά της:

Καταιγίδα	Βροχή	Συννεφιά	Ήλιος

Μια μέρα, οι κάστορες στην πεδιάδα βλέπουν το παρακάτω μήνυμα:

Κάτι πήγε στραβά! Η Μετεωρολόγος έστειλε κατά λάθος ένα μικρό σύννεφο αντί για ένα μεγάλο, ή ένα μεγάλο σύννεφο αντί για ένα μικρό. 

Ερώτηση:
Ποιο ήταν το μήνυμα για τον καιρό που ήθελε να στείλει αρχικά?

Απάντηση:
Α. Καταιγίδα
Β. Βροχή
Γ. Συννεφιά
Δ. Ήλιος

Λύση:
Η απάντηση Γ είναι σωστή.

Εξήγηση:
Με δεδομένο πως στο μήνυμα της Μετεωρολόγου υπήρχε μόνο ένα λάθος, μπορούμε να φτάσουμε στο συμπέρασμα πως η μόνη σωστή απάντηση μπορεί να είναι το Γ (Συννεφιά). Παρατηρούμε πως για να αποκωδικοποιηθεί το μήνυμα ως Καταιγίδα, Βροχή ή Ήλιος θα χρειαστούν περισσότερες από μία μετατροπές, ενώ για να αποκωδικοποιηθεί το μήνυμα ως Συννεφιά θα χρειαστεί μόνο μία, όσο δηλαδή και ο αριθμός των λάθων που γνωρίζουμε ότι έγιναν.

Σκουπιδο-Ρομπότ

(Βαθμός δυσκολίας: Εύκολο)

Στην εικόνα βλέπετε τον χάρτη ενός πάρκου που είναι χωρισμένο σε τετράγωνα.

Σε κάθε τετράγωνο φαίνεται πόσα σκουπίδια άφησαν εκεί οι επισκέπτες.

Οι φύλακες του πάρκου έχουν δυο ρομπότ, τον Anton και τον Boris, που μαζεύουν όλα τα σκουπίδια που βρίσκουν σε ένα τετράγωνο όταν μπουν σε αυτό.

Στα ρομπότ δίνονται οι παρακάτω εντολές:

Πρώτα, το ρομπότ Anton να πάει: 

Στη συνέχεια, το ρομπότ Boris να πάει: 

Ερώτηση:
Πόσα κομμάτια σκουπιδιών θα μαζέψει τελικά το ρομπότ Boris;

Απάντηση:
Α. 3
Β. 9
Γ. 11
Δ. 12

Λύση:
Η απάντηση Β είναι σωστή.

Εξήγηση:
Το ρομπότ Anton θα μαζέψει 1+2+0 κομμάτια σκουπιδιών, δηλαδή 3 συνολικά κομμάτια με τις οδηγίες που του δώθηκαν.
Έπειτα, το ρομπότ Boris θα μαζέψει 3+6+0 κομμάτια σκουπιδιών, δηλαδή 9 συνολικά κομμάτια με τις οδηγίες που του δώθηκαν.
Παρατηρούμε πως αν το ρομπότ Boris ξεκίναγε την διαδρομή του πρώτο θα είχε μαζέψει 3+6+2 κομμάτια, όμως στην περίπτωση μας, το ρομπότ Anton είχε ήδη μαζέψει αυτά τα 2 κομμάτια.

Σύστημα Quipu

(Βαθμός δυσκολίας: Δύσκολο)

Η πρόεδρος των καστόρων, αφού γύρισε από ένα επίσημο ταξίδι στο Περού, κάνει ανακοινώσεις δένοντας κόμπους σε κρεμασμένα σχοινιά (το σύστημα αυτό ονομάζεται Quipu, προφέρεται Κχίπου, και σημαίνει “τα σχοινιά που μιλάνε”).
Το παρακάτω μήνυμα Quipu σημαίνει “ας γιορτάσουμε”:

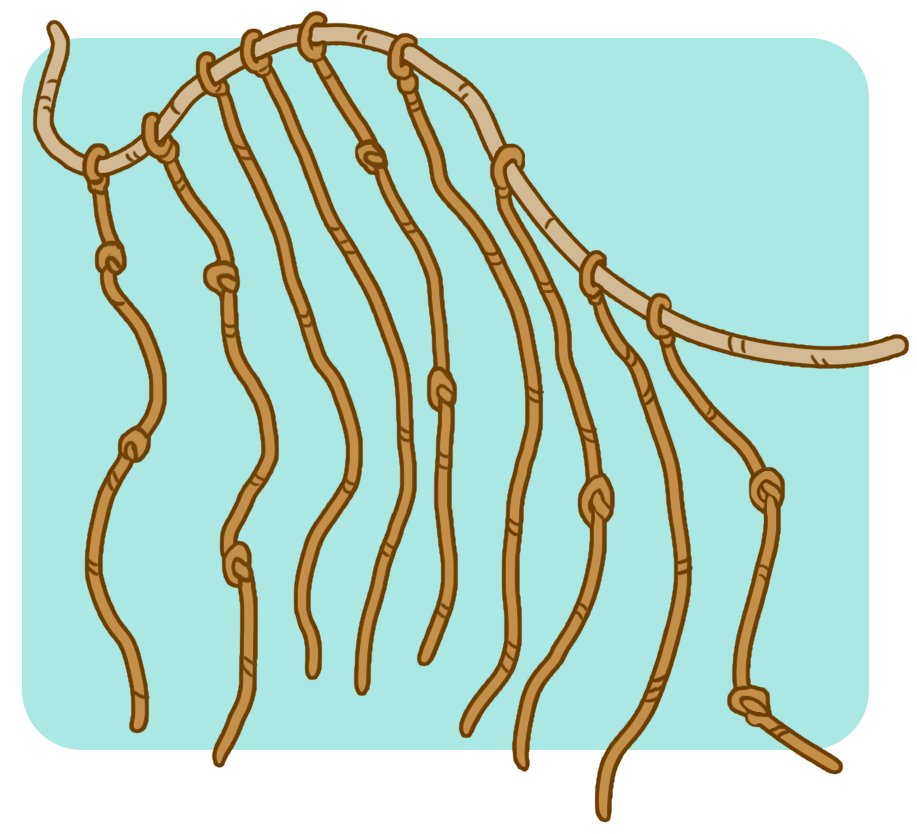
Πιστεύει όμως ότι είναι πολύ δύσκολο να θυμάται κάποιος όλα τα διαφορετικά μηνύματα.
Η πρόεδρος χρειάζεται να κάνει μόνο 50 διαφορετικές ανακοινώσεις, και θέλει ένα καινούριο σύστημα Quipu με λιγότερα σχοινιά.

Το μόνο που έχει σημασία για το κάθε μήνυμα είναι η σειρά των σχοινιών και ο αριθμός των κόμπων που έχει κάθε σχοινί. 
Το κάθε σχοινί μπορεί να έχει 0, 1, 2 ή 3 κόμπους.

Ερώτηση:
Ποιος είναι ο ελάχιστος αριθμός σχοινιών που θα πρέπει να έχει το καινούριο σύστημα Quipu ώστε να μπορούν να δημιουργηθούν 50 διαφορετικά μηνύματα;

Απάντηση:
Α. 2 σχοινιά
Β. 3 σχοινιά
Γ. 4 σχοινιά
Δ. 5 σχοινιά

Λύση:
Η απάντηση Β είναι σωστή.

Εξήγηση:
Για την επίλυση του παραπάνω προβλήματος θα προσπαθήσουμε να υπολογίσουμε πόσα διαφορετικά μηνύματα μπορούμε να δημιουργήσουμε ξεκινώντας από το ένα σχοινί μέχρι να φτάσουμε τα 50 μηνύματα.
Με ένα μόνο σχοινί θα έχουμε 4 διαφορετικά μηνύματα, δηλαδή κάθε κόμπος θα αντιστοιχεί σε ένα μήνυμα.
Με δύο σχοινία θα επιλέγουμε έναν αριθμό κόμπων για το πρώτο σχοινί και θα μετράμε όλους τους συνδυασμούς μηνυμάτων που κάνει με το δεύτερο σχοινί:

Σχοινί 1: 0 κόμποι | Σχοινί 2: 0, 1, 2, 3 κόμποι -> 4 μηνύματα
Σχοινί 1: 1 κόμπος | Σχοινί 2: 0, 1, 2, 3 κόμποι -> 4 μηνύματα
Σχοινί 1: 2 κόμποι | Σχοινί 2: 0, 1, 2, 3 κόμποι -> 4 μηνύματα
Σχοινί 1: 3 κόμποι | Σχοινί 2: 0, 1, 2, 3 κόμποι -> 4 μηνύματα

Δηλαδή συνολικά 4+4+4+4 = 16 μηνύματα. Μπορούμε να συνεχίσουμε έτσι ή πολύ πιο εύκολα να μετατρέψουμε την διαδικασία σε μαθηματικά! Παρατηρούμε πως ο αριθμός των μηνυμάτων είναι ίσος με τον αριθμό των πιθανών κόμπων σε ένα σχοινί (4) υψωμένος στον αριθμό των σχοινιών:
– Για ένα σχοινί: 4¹ = 4 μηνύματα
– Για δύο σχοινιά: 4² = 16 μηνύματα

Άρα, πολύ εύκολα καταλήγουμε πως 3 σχοινιά είναι αρκετά αφού:
4³ = 4 x 4 x 4 = 4 x 16 = 64 μηνύματα

Πλέγματα τρίλιζας

(Βαθμός δυσκολίας: Μέτριο)

Η τρίλιζα είναι ένα επιτραπέζιο παιχνίδι 2 παικτών.

Κάνονες τρίλιζας:
Το παιχνίδι πραγματοποιείται σε ένα πλέγμα 3×3 όπου δύο παίκτες ανταγωνίζονται, ο ένας ως “Χ” και ο άλλος ως “Ο”. Πρώτα παίζει ο παίκτης “Χ”. Οι παίκτες τοποθετούν τα σύμβολά τους εναλλάξ σε ελεύθερα τετράγωνα και δεν επιτρέπεται να παραλείψουν τον γύρο τους. Ο στόχος των παικτών είναι να σχηματίσουν τρία ίδια σύμβολα σε μια σειρά – κάθετα, οριζόντια ή διαγώνια. Αν κάποιος παίκτης σχηματίσει τρία ίδια σύμβολα, το παιχνίδι τελειώνει. Τέλος, αν όλα τα τετράγωνα είναι γεμάτα και κανείς δεν έχει φτιάξει μια σειρά τριών συμβόλων, το παιχνίδι θεωρείται ισόπαλο.

Παράδειγμα παιχνιδιού:

Στο παραπάνω παιχνίδι, νικητής ήταν ο παίκτης Χ και το τελευταίο πλέγμα που φαίνεται αποτελεί ένα έγκυρο τελικό πλέγμα τρίλιζας.
Αν το 3×3 πλέγμα γεμίσει με τυχαία σύμβολα, δεν είναι απαραίτητο πως θα είναι και έγκυρο σύμφωνα με τους κανόνες.

Ερώτηση:
Ποιο από τα παρακάτω τελικά πλέγματα είναι έγκυρο σύμφωνα με τους κανόνες της τρίλιζας;

Απάντηση:
Α.

Β.

Γ.

Δ.

Λύση
Η απάντηση Γ είναι σωστή.

Εξήγηση:
Ο πιο απλός τρόπος επίλυσης του προβλήματος είναι να ακολουθήσουμε την πορεία των δύο παικτών μέχρι να παρατηρήσουμε κάποιο λάθος.
Αλλιώς, μπορούμε να αντλήσουμε κριτήρια για την εγκυρότητα των τελικών πλεγμάτων από τους κανόνες του παιχνιδιού:

Κανόνας: Ο παίκτης “Χ” παίζει πρώτος. Άρα,
→ Ο παίκτης “Χ” θα έχει πάντα ίσα ή περισσότερα σύμβολα στο πλέγμα από τον παίκτη “Ο”. Δηλαδή, η απάντηση Α είναι λανθασμένη, αφού υπάρχουν περισσότερα “Ο” από “Χ” στο πλέγμα.

Κανόνας: Οι παίκτες παίζουν εναλλάξ και δεν μπορούν να παραλείψουν τον γύρο τους. Άρα,
→ Οι παίκτες θα έχουν το πολύ διαφορά πλήθους ενός σύμβολου σε κάθε περίπτωση. Δηλαδή, η απάντηση Β είναι λανθασμένη, αφού υπάρχουν 2 περισσότερα “Χ” από “Ο” στο πλέγμα.

Κανόνας: Το παιχνίδι δεν τελειώνει μέχρι να κερδίσει κάποιος παίκτης ή να υπάρξει ισοπαλία. Άρα,
→ Δεν μπορεί να υπάρξει έγκυρο τελικό πλέγμα εφόσον κάποιος παίκτης δεν έχει κερδίσει ή το πλέγμα δεν είναι ολοκληρωμένο. Δηλαδή, η απάντηση Δ είναι λανθασμένη.

Ιός υπολογιστή

(Βαθμός δυσκολίας: Δύσκολο)

Στο παρακάτω διάγραμμα οι κύκλοι είναι υπολογιστές και οι γραμμές είναι οι συνδέσεις μεταξύ τους.

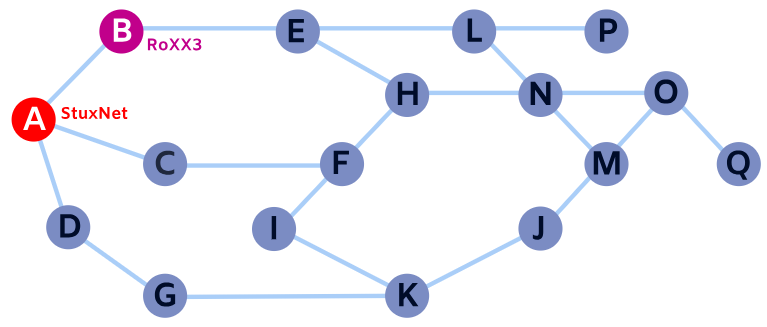
Ο υπολογιστής Α είναι μολυσμένος από τον ίο StuxNet και ο υπολογιστής Β είναι μολυσμένος από τον ιό RoXX3.
Κάθε μέρα, οι δύο ιοί εξαπλώνονται από τους μολυσμένους υπολογιστές σε όλους τους υπόλοιπους γειτονικούς υπολογιστές, σύμφωνα με το διάγραμμα συνδέσεων. Εάν ένας υπολογιστής μολυνθεί και από τους δύο ιούς τότε καταστρέφεται και δεν μπορεί να μεταδώσει τον ιό ή να μολυνθεί ξανά.
Μετά από μερικές μέρες, κάθε υπολογιστής θα είναι μολυσμένος ή κατεστραμένος.

Ερώτηση:
Πόσοι υπολογιστές θα είναι λειτουργικοί αλλά μολυσμένοι από τον ιό RoXX3 μετά από μία εβδομάδα;

Απάντηση:
Α. 6 υπολογιστές
Β. 7 υπολογιστές
Γ. 8 υπολογιστές
Δ. 9 υπολογιστές
Ε. 10 υπολογιστές

Λύση:
Η απάντηση Α είναι σωστή.

Εξήγηση:
Ακολουθούμε την πορεία μετάδωσης και των δύο ιών ανά μέρα. Τελικά, την μέρα 5 θα φτάσουμε στην παρακάτω κατάσταση:

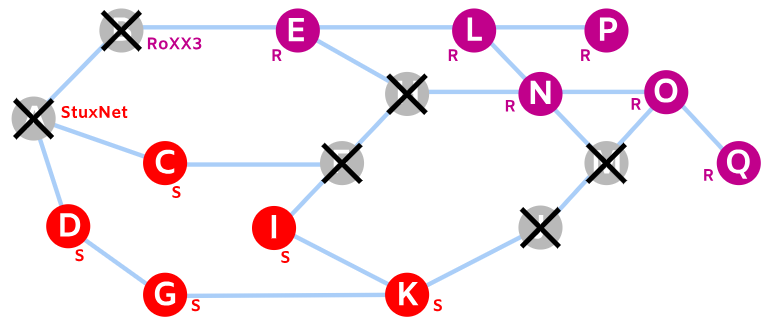
Παρατηρούμε πως πλέον δεν υπάρχει τρόπος για έναν υπολογιστή να μολυνθεί και από τους δύο ιούς αφού οι κατεστραμμένοι υπολογιστές έχουν κλείσει κάθε πιθανό μονοπάτι. Επομένως, η παραπάνω κατάσταση θα παραμείνει ίδια μέχρι να φτάσουμε στην 7η μέρα.